前几天和德川一起在学习会上讲解了k-NN算法，这里进行总结一下，力争用最通俗的语言讲解以便有利于更多同学的理解本文目录如下：1.k近邻算法的基本概念，原理以及应用2.k近邻算法中k的选取，距离的度量以及特征归一化的必要性。

3.k近邻法的实现：kd树原理的讲解4.kd树详细例子讲解5.kd树的不足以及最差情况举例6.k近邻方法的一些个人总结一.k近邻算法的基本概念，原理以及应用k近邻算法是一种基本分类和回归方法本篇文章只讨论分类问题的k近邻法。

K近邻算法，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中（这就类似于现实生活中少数服从多数的思想）根据这个说法，咱们来看下引自维基百科上的一幅图：。

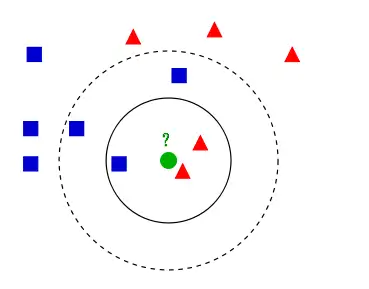
如上图所示，有两类不同的样本数据，分别用蓝色的小正方形和红色的小三角形表示，而图正中间的那个绿色的圆所标示的数据则是待分类的数据这也就是我们的目的，来了一个新的数据点，我要得到它的类别是什么？好的，下面我们根据k近邻的思想来给绿色圆点进行分类。

如果K=3，绿色圆点的最邻近的3个点是2个红色小三角形和1个蓝色小正方形，少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于红色的三角形一类如果K=5，绿色圆点的最邻近的5个邻居是2个红色三角形和3个蓝色的正方形，。

还是少数从属于多数，基于统计的方法，判定绿色的这个待分类点属于蓝色的正方形一类从上面例子我们可以看出，k近邻的算法思想非常的简单，也非常的容易理解，那么我们是不是就到此结束了，该算法的原理我们也已经懂了，也知道怎么给新来的点如何进行归类，只要找到离它最近的k个实例，哪个类别最多即可。

哈哈，没有这么简单啦，算法的核心思想确实是这样，但是要想一个算法在实际应用中work，需要注意的不少额~比如k怎么确定的，k为多少效果最好呢？所谓的最近邻又是如何来判断给定呢？哈哈，不要急，下面会一一讲解！

二.k近邻算法中k的选取以及特征归一化的重要性 选取k值以及它的影响k近邻的k值我们应该怎么选取呢？如果我们选取较小的k值，那么就会意味着我们的整体模型会变得复杂，容易发生过拟合！恩~结论说完了，太抽象了吧你，不上图讲解号称通俗讲解的都是流氓

~好吧，那我就上图来讲解假设我们选取k=1这个极端情况，怎么就使得模型变得复杂，又容易过拟合了呢？假设我们有训练数据和待分类点如下图：

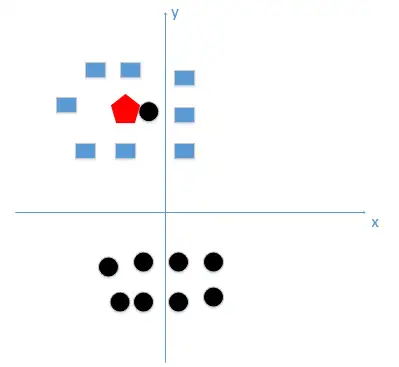
上图中有俩类，一个是黑色的圆点，一个是蓝色的长方形，现在我们的待分类点是红色的五边形好，根据我们的k近邻算法步骤来决定待分类点应该归为哪一类我们由图中可以得到，很容易我们能够看出来五边形离黑色的圆点最近，k又等于1，那太好了。

，我们最终判定待分类点是黑色的圆点由这个处理过程我们很容易能够感觉出问题了，如果k太小了，比如等于1，那么模型就太复杂了，我们很容易学习到噪声，也就非常容易判定为噪声类别，而在上图，如果，k大一点，k等于8，。

把长方形都包括进来，我们很容易得到我们正确的分类应该是蓝色的长方形！如下图：

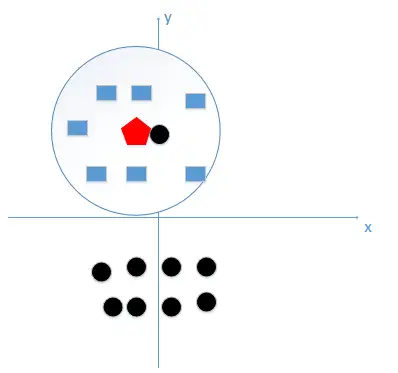
所谓的过拟合就是在训练集上准确率非常高，而在测试集上准确率低，经过上例，我们可以得到k太小会导致过拟合，很容易将一些噪声（如上图离五边形很近的黑色圆点）学习到模型中，而忽略了数据真实的分布！如果我们选取较大的k值，就相当于用较大邻域中的训练数据进行预测，这时与输入实例较远的（不相似）训练实例也会对预测起作用，使预测发生错误，k值的增大意味着整体模型变得简单。

k值增大怎么就意味着模型变得简单了，不要急，我会解释的！哈哈我们想，如果k=N（N为训练样本的个数）,那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类这时，模型是不是非常简单，这相当于你压根就没有训练模型呀！。

直接拿训练数据统计了一下各个数据的类别，找最大的而已！这好像下图所示：

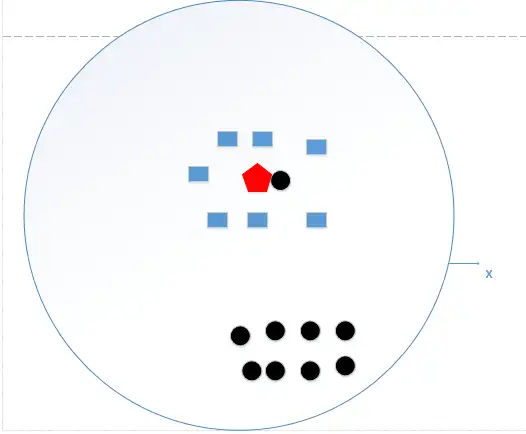
我们统计了黑色圆形是8个，长方形个数是7个，那么哈哈，如果k=N，我就得出结论了，红色五边形是属于黑色圆形的（明显是错误的好不，捂脸！）这个时候，模型过于简单，完全忽略训练数据实例中的大量有用信息，是不可取的。

恩，k值既不能过大，也不能过小，在我举的这个例子中，我们k值的选择，在下图红色圆边界之间这个范围是最好的，如下图：

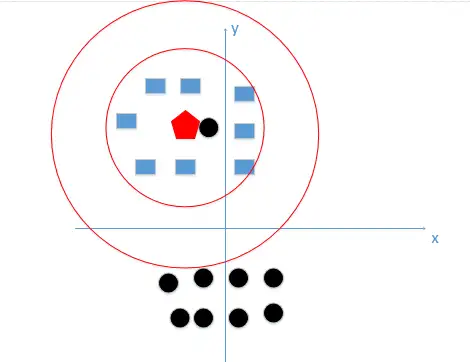
（注：这里只是为了更好让大家理解，真实例子中不可能只有俩维特征，但是原理是一样的1，我们就是想找到较好的k值大小）那么我们一般怎么选取呢？李航博士书上讲到，我们一般选取一个较小的数值，通常采取 交叉验证法来选取最优的k值。

（也就是说，选取k值很重要的关键是实验调参，类似于神经网络选取多少层这种，通过调整超参数来得到一个较好的结果） 2.距离的度量在上文中说到，k近邻算法是在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，我们就说预测点属于哪个类。

定义中所说的最邻近是如何度量呢？我们怎么知道谁跟测试点最邻近。这里就会引出我们几种度量俩个点之间距离的标准。我们可以有以下几种度量方式：

其中当p=2的时候，就是我们最常见的欧式距离，我们也一般都用欧式距离来衡量我们高维空间中俩点的距离在实际应用中，距离函数的选择应该根据数据的特性和分析的需要而定，一般选取p=2欧式距离表示，这不是本文的重点。

恩，距离度量我们也了解了，下面我要说一下各个维度归一化的必要性！ 3.特征归一化的必要性首先举例如下，我用一个人身高(cm)与脚码（尺码）大小来作为特征值，类别为男性或者女性我们现在如果有5个训练样本，分布如下：。

A [(179,42),男] B [(178,43),男] C [(165,36)女] D [(177,42),男] E [(160,35),女]通过上述训练样本，我们看出问题了吗？很容易看到第一维身高特征是第二维脚码特征的4倍左右，那么在进行距离度量的时候，

我们就会偏向于第一维特征这样造成俩个特征并不是等价重要的，最终可能会导致距离计算错误，从而导致预测错误口说无凭，举例如下：现在我来了一个测试样本 F(167,43)，让我们来预测他是男性还是女性，我们采取k=3来预测。

下面我们用欧式距离分别算出F离训练样本的欧式距离，然后选取最近的3个，多数类别就是我们最终的结果，计算如下：

由计算可以得到，最近的前三个分别是C,D,E三个样本，那么由C,E为女性，D为男性，女性多于男性得到我们要预测的结果为女性这样问题就来了，一个女性的脚43码的可能性，远远小于男性脚43码的可能性，那么为什么算法还是会预测F为女性呢？那是因为由于各个特征量纲的不同，在这里导致了身高的重要性已经远远大于脚码了，这是不客观的。

所以我们应该让每个特征都是同等重要的！这也是我们要归一化的原因！归一化公式如下：

讲到这里，k近邻算法基本内容我们已经讲完了除去之后为了提高查找效率提出的kd树外，算法的原理，应用等方面已经讲解完毕，由于每篇文章内容不宜太多，kd树等知识下篇讲解，这里总结一下本文讲的内容三.本文的一点总结。

1.我们提出了k近邻算法，算法的核心思想是，即是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的K个实例，这K个实例的多数属于某个类，就把该输入实例分类到这个类中更通俗说一遍算法的过程，来了一个新的输入实例，我们算出该实例与每一个训练点的距离（这里的复杂度为0(n)比较大，所以引出了下文的kd树等结构），然后找到前k个，这k个哪个类别数最多，我们就判断新的输入实例就是哪类！。

2.与该实例最近邻的k个实例，这个最近邻的定义是通过不同距离函数来定义，我们最常用的是欧式距离3.为了保证每个特征同等重要性，我们这里对每个特征进行归一化4.k值的选取，既不能太大，也不能太小，何值为最好，需要实验调整参数确定！。

本文讲解结束了，真心希望对大家理解有帮助！欢迎大家指错交流~参考：李航博士《统计学习方法》【量化课堂】一只兔子帮你理解 kNN从K近邻算法、距离度量谈到KD树、SIFT+BBF算法 - 结构之法 算法之道 - 博客频道 - CSDN.NET

致谢：德川，继豪，皓宇，施琦