1.微分方程的解之通解，特解，奇解通解：指的是含有任意常数，且常数个数和微分方程阶数相同的解特解：指的是在初值条件确定后，明确了各个常数的具体值时的一个解奇解：同济教材并没有给出特别的阐述，考题也未涉及，所以可以不管。

解可以以显函数或是隐函数的形式给出，如果能够化成显函数的形式就化为显函数的形式。2.通解的任意常数的含义Q:任意常数是说C可以取任意值吗?A:这样的理解是不正确的。考虑如下题目。

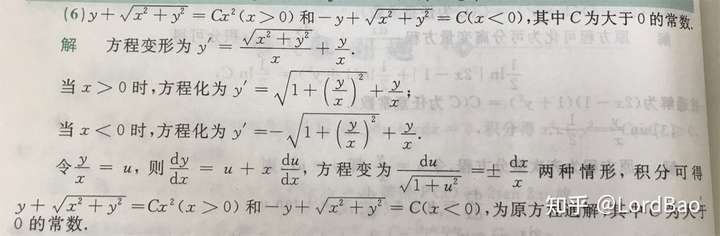
这是知乎朋友 @Laity 提的一个问题，看答案你会发现C是大于0的常数，所以不能浅显地认为C可以取任意值事实上，通解的任意常数的真正含义是:以可分离变量的微分方程为例，假设f(x),g(x)f(x),g(x)。

可积，并且各自的原函数为F(x),G(x)F(x),G(x),那么:对 f(u)du=g(x)dxf(u)mathrm d u = g(x) mathrm d x 两边积分可以得到 F(u)=G(

x)+φ(c)F(u) =G(x) +arphi(c) ，这个 φ(c)arphi(c) 是 ln⁡Cln C,CC ，还是tan⁡C an C 都没问题，重点是φ(c)arphi(c)

是任意常数，而 ln⁡Cln C,CC ，还是tan⁡C an C的目的仅仅是为了后续好处理罢了这才是任意常数的真正意思3.是什么让我们误以为C取任意常数?这个误导最开始来源于可分离变量的漏解问题。

。

我们经常迷惑的东西就是上面那个 ln⁡y=Cxln y =C x 的C就是取任意值千万注意， 0) ">ln⁡|ln⁡y|=ln⁡|C1x|(C1>0)ln |ln y|= ln |C_1 x| (C_1>0) 。

就已经是通解了，通解是一类形式解你写成 ln⁡y=±C1xln y = pm C_1 x 也可以但是我们为了让形式更加完整，考虑了漏解的情况，这样就可以写成ln⁡y=Cxln y =Cx 这个的依据来自于。

那么ln⁡y=Cxln y =C x是否可以进一步写成y=C2exy = C_2 e^x呢?答案是不能，这个C2C_2并不能替换ece^c,因为换成C2C_2是有依据的，如果C2=0C_2=0，那么

y=0y=0但事实上，y是不能取0的，所以不可以写成y=C2exy=C_2e^x的微分方程有很多类似的题目，但不是每一个题目都会漏解比如dy1+y2=dxxrac{mathrm dy}{sqrt{1+y^2}}=rac{mathrm d x}{ x}。

.对两边求积分可得0)">ln⁡(y+1+y2)=ln⁡|x|+ln⁡C1(C1>0)ln (y + sqrt{1+y^2})=ln |x| + ln C_1 (C_1>0).那么y+1+y2)

=±C1xy + sqrt{1+y^2})= pm C_1x为什么这里不考虑不写成y+1+y2=Cxy + sqrt{1+y^2}= Cx呢？因为0">1+y2>0sqrt{1+y^2} >0。

的，根本就不存在漏解情况。4.漏解和增解的问题漏解求通解的时候，可以不用考虑漏解。而初值条件问题，就需要考虑漏解。

增解

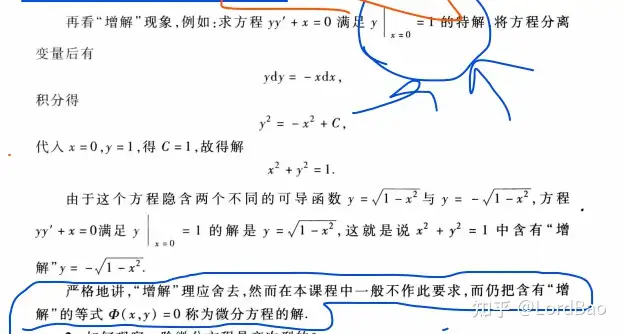
根据同济教材的解释,上述题解可以写成x2+y2=1x^2+y^2=1，虽然存在增解，但是它却含有我们想要的特解这么做是有理由的因为有时候我们能难或是不能从隐函数中拿到关于y的显函数，考虑x4+y4=1x^4 + y^4=1

.但是，就目前考研的题目来看，这种简单的x2+y2=1x^2+y^2=1还是化为y=x2+1y = sqrt{x^2+1}比较好。5.并不是所有微分方程都有通解。

微分方程的通解并不是所有解。但特别地，线性微分方程的通解即为任意解(这个以后再说)。

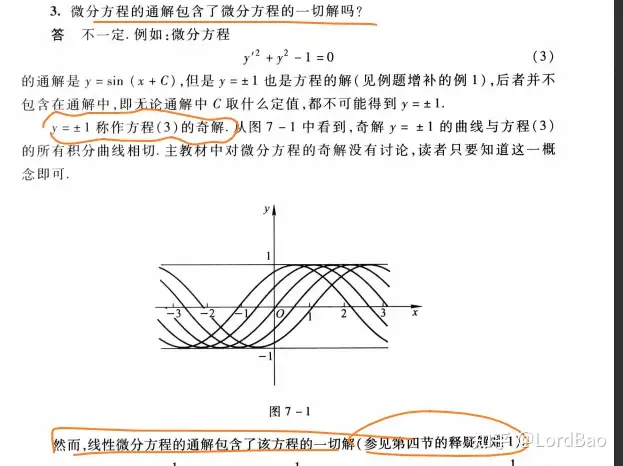
6.函数在不同区域上的通解

通解，更确切来说函数在不同区域上的通解。e.g

7.参考书籍同济高等数学第7版同济高等数学学习辅导和习题讲解第7版