欢迎关注，微信公众号“CN分享”http://weixin.qq.com/r/4ziIkJjEYsUdrdzz923x (二维码自动识别)今天，我们聊一个有意思的问题——尺规作图尺规作图起源于古希腊的数学课题，欧几里得的《几何原本》将其规范 ，借助《几何原本》的巨大影响，一直流传至今，并对现代数学的发展起了很大的推动作用，特别是对近代的方程论、群论等数学分支。

(欧几里得与几何原本)定义：尺规作图，简单理解起来就是指用直尺和圆规作图，但此直尺是无刻度的，圆规也无刻度，而且必须是有限次。

下面给出尺规作图的准确定义尺规作图定义：承认以下五项前提，有限次运用以下五项公法而完成的作图方法，就是合法的尺规作图：五项前提是：(1) 允许在平面上、直线上、圆弧线上已确定的范围内任意选定一点（所谓“确定范围”，依下面四条的规则）。

(2) 可以判断同一直线上不同点的位置次序(3) 可以判断同一圆弧线上不同点的位置次序(4) 可以判断平面上一点在直线的哪一侧(5) 可以判断平面上一点在圆的内部还是外部五项公法是：(1) 根据两个已经确定的点作出经过这两个点的直线。

(2) 以一个已经确定的点为圆心，以两个已经确定的点之间的距离为半径作圆(3) 确定两个已经做出的相交直线的交点(4) 确定已经做出的相交的圆和直线的交点(5) 确定已经做出的相交的两个圆的交点著名问题：

在尺规作图的发展中，出现了三个比较著名的问题：1.尺规作图不能问题（倍立方，化圆为方，三等分角）2.作正多边形3.四等分圆角本次，我们就其中的2也就是正多边形的画法，展开相应的讨论在正式开始之前，我们先做一下准备工作，来了解一个由“数学王子”高斯提出来的定理。

定理：尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积。这是尺规作图正多变形的充要条件，其中费马数是以数学家费马命名一组自然数，具有形式(2^(2^n)+1 )

（费马素数）

（费马）故可以用尺规作图画出的正多边有：2²:4,8,16;费马数:3,5,17;

两者的乘积:6,10,12;所以正7,9,11,13,14,15是不能用尺规作图实现，对这六个正多边形，我们采用近似的画法来实现好，下面我们开动了：第一大类：我们先看第一大类不能用尺规作图实现而采用近似画法的正7,9,11,13,14,15边形。

正七边形:近似正七边形的作法：

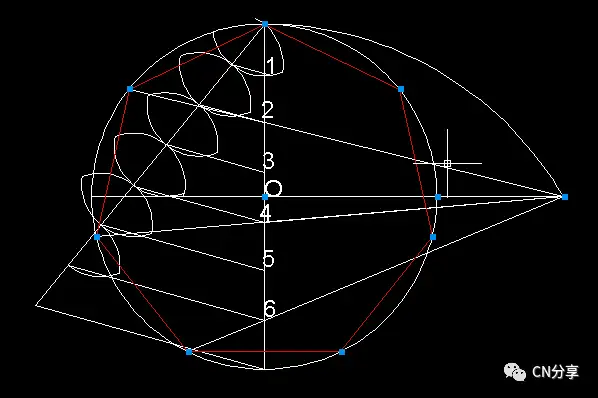
1，以圆心O，定长R为半径画圆，并作出两条互相垂直的直径MN，AP2，七等分直径MN3，以M为圆心，MN为半径画弧，交OA延长线于A1，交OP延长线于P14，将A1，P1与直径上第2，4，6个等分点并延长，交圆周于B，C，D，E，F，G。

5，连接MBCDEFG则得正七边形这是一个近似的做法改进：由4步确定边长改为3 步确定边长1；作圆，圆心为O2；作弦长为半径大小的弦AB3；作弦AB的中垂线，垂足为C4；以OC为长度单位（OC即是所作正七边形边长），划分圆，并连接各分点，即是所求正七边形。

正九边形，正十一边形，正十三边形，正十四边形，正十五边形只需将以上的MN等分成相应的份数，然后画弧，延长，相交，连接，即可，对于正十四边形还可以通过对正七边每条边等分即可得。

（正九边形）

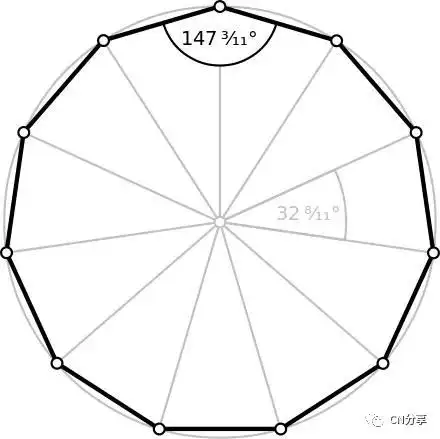
（正十一边形）

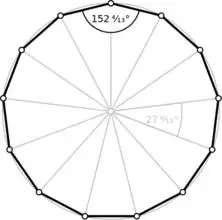
（正十三边形）

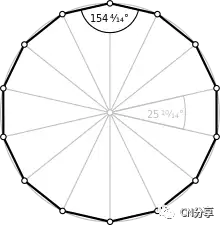
（正十四边形）

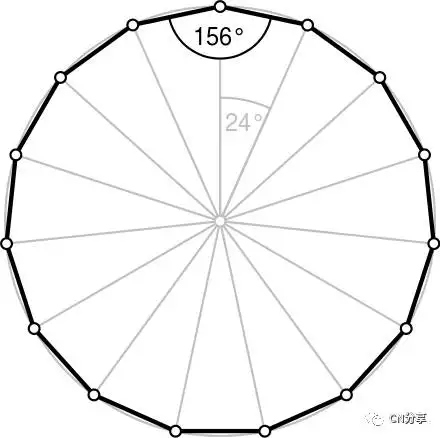
（正十五边型）第二大类：可以用尺规作图实现的正多边形正三边形：

（1）做任意长度线段AB（2）分别以A、B为圆心，以AB长为半径画弧，两弧交于一点C（3）连接AC、BC则三角形ABC即为所求正四边形：

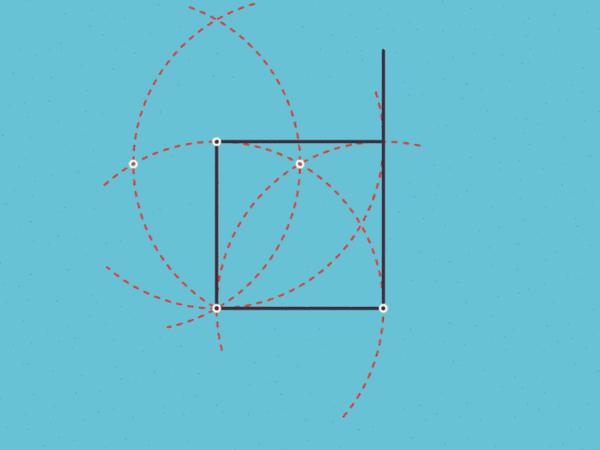
正四边形:用圆规做圆,过圆心做互相垂直的直径,依次连接直径与圆的交点正五边形：

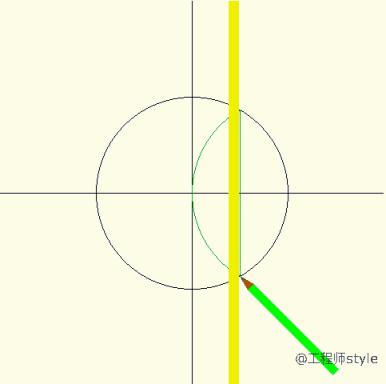
①以O为圆心,定长R为半径画圆,并作互相垂直的直径MN和 AP.　　② 平分半径ON,得OK=KN.　　③以 K为圆心,KA为半径画弧与 OM交于 H, AH即为正五边形的边长.　　④以AH为弦长,在圆周上截得A,B,C,D,E各点,顺次连接这些点即得正五边形.

对于6,8,10,12我们可以通过相应的1/2边即3,4,5,6再平分即可得，正16边形方法类似。

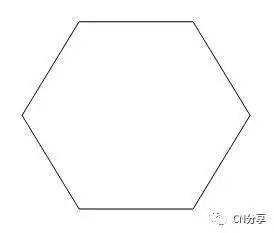
（正六边形）

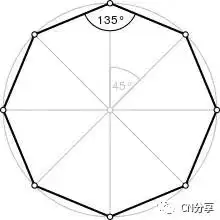
（正八边形）

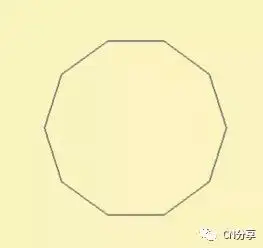
（正十边形）

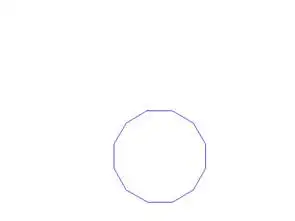
（正十二边形）经过一番跋涉，我们终于来到了最后一个，也是最难的一个——正十七边形

先看图

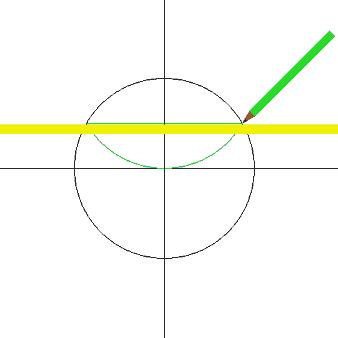
看完之后，你是否是这样？

不急，我们慢慢说1.给一圆O，作两垂直的直径AB、CD.2.在OA上作E点使OE=1/4AO,连结CE. 3.作∠CEB的平分线EF.　　4.作∠FEB的平分线EG,交CO于P.　　5.作∠GEH=45°,交CD于Q.

　　6.以CQ为直径作圆,交OB于K.　　7.以P为圆心,PK为半径作圆,交CD于L、M.　　8.分别过M、L作CD的垂线,交圆O于N、R.　　9.作弧NR的中点S,以SN为半径将圆O分成17等份.

看完了，来听个故事：一天晚上，19岁正读博的高斯的导师由于疏忽将两千多年未解决的一个问题——尺规做正十七边形留给了高斯，高斯优哉游哉得咬着笔头写着作业，然后表情严肃起来，妈的这题有点BT啊！想啊想，通宵一晚，伴着拂晓的晨光，高斯铅笔一扔，胸口长舒一口气。

心说，唉，最近智商又下降了，想我9岁算1+2+3……+100也没用这么长时间啊，这么个破题居然花了一晚上时间！第二天拿给博导，博导惊了，对他说，这可是阿基米德牛顿都没做出来的题啊！你真是个天才啊！后来高斯给出了尺规作图正多变形的充分必要条件，也就是刚开始的那个定理。

（“迷之微笑”的高斯）编辑不容易，欢迎关注。微信公众号：CN分享。