在闭环控制策略中，PID控制由于结构简单，因此应用最为广泛当然大量的文章也一次又一次的介绍这种经典的控制方法，为了补充专栏中控制理论的体系，且PID控制对于初学者如此的不可或缺，因此对于很有必要花几天时间写一下自己对PID控制的理解，并着重对实际数字化PID控制器中存在的问题进行了分析，如有不对之处，欢迎指正。

在专栏中补充完控制理论后，对电机控制驱动策略逐一进行分析为了方便大家下载，相关代码已上传到GitHub，后续我会继续添加新的模型和代码在这上面GIT HUB的SSH为：git@github.com:Seanxinyuan/Resources.git。

GIT HUB的HTTP为：https://github.com/Seanxinyuan/Resources.git强烈推荐大家用SSH方式下载代码和模型，便于后续管理；如果有不明白之处，欢迎咨询，我会提供一份GITHUB 指南。

本文目录如下所示：控制系统概念P比例控制I积分控制D微分控制PID控制实际PID控制器中存在问题总结控制系统概念在谈及控制系统，我们如何科学地进行设计呢？这是控制系统这门课的核心再设计之前需要给出设计控制系统的五个步骤：。

控制系统需求了解被控对象的数学模型选择合适的控制策略调节控制策略中相关参数验证控制策略是否满足需求1.控制系统需求→2.了解被控对象的数学模型→3.选择合适的控制策略⇓→4.调节控制策略中相关参数→5.

验证控制策略是否满足需求1. 控制系统需求 ightarrow2. 了解被控对象的数学模型 ightarrow3. 选择合适的控制策略\ Downarrow\ ightarrow4. 调节控制策略中相关参数 ightarrow5. 验证控制策略是否满足需求

因此在第三阶段的控制策略中，可以分为开环控制和闭环控制。开环控制：

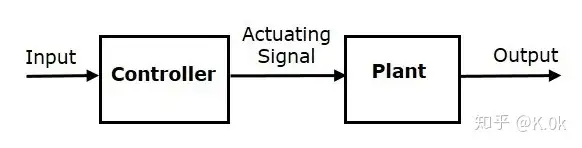
这种方法理解简单且易维护，然而这种方法的鲁棒性较差，其次这种方法只追求输出量和输入量的关系，系统的动态响应速度不可控。闭环控制：

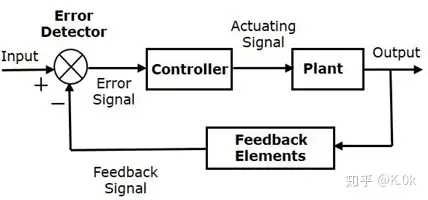
这种方法可以根据目标量和实际输出量的偏差来进行合理的控制，系统更加可靠，其次，基于闭环控制，动态性能也可以进行控制参考下述这个传送门来证明闭环控制具有较好鲁棒性：Using Bode Plots, Part 1: Closed-Loop Systems - Video。

​www.mathworks.com/videos/using-bode-plots-closed-loop-systems-1-of-5-77057.html假设系统存在外部扰动 dd 和测量反馈扰动信号

nn ,我们重新构建结构图和传递函数如下所示：

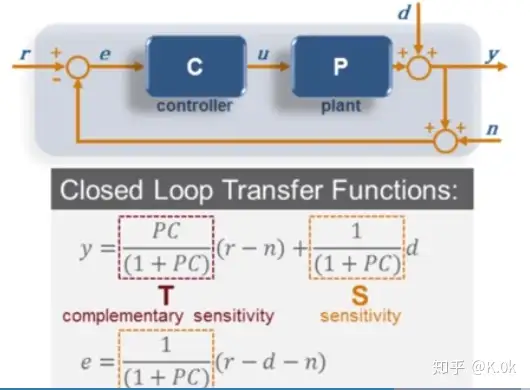
可以看出当选择合适的控制器传递函数，稳态误差依然可以为零。根据叠加原理，在输出变量中两部分组成T和S，分别进行T和S所对应的传递函数闭环Bode图：T传递函数Bode图：

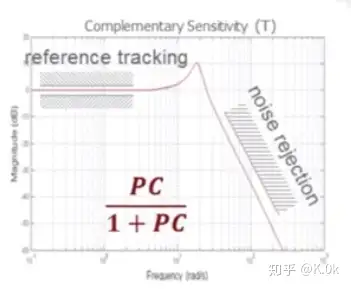
可以看出，闭环系统可以保持对输入 rr 和测量反馈扰动低频信号 nn 进行完全跟踪（信号频率小于截止频率），对输入 rr 和测量反馈扰动高频信号 nn 进行抑制。S传递函数Bode图：

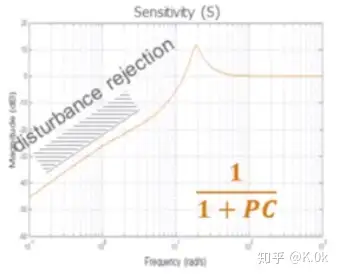
可以看出，闭环系统可以保持对外部扰动 dd的高频信号进行完全跟踪，对外部扰动 dd的低频信号进行抑制综上所述，闭环系统具有一定的抗扰动能力这里我们再从另一个维度来说明，在T传递函数中，也可以反映出PC增益越大，实际输出量 。

yy 可以跟随给定值 、噪声r、噪声nr、噪声n ,而PC增益越小，实际输出量 yy可以有效的抑制给定值 、噪声r、噪声nr、噪声n，通过这一个逻辑关系，我们理想的需求是在PC幅值增益较大时( >1">

PC>>1PC>>1 )所对应的信号频率低，进而来迫使实际输出量 yy 可以跟随给定值 rr，在PC幅值增益较小时（ PC<<1PC<<1 ）所对应的信号频率高，进而可以抑制高频的噪声同理，在S传递函数中，当PC幅值增益越大，实际输出量 。

yy可以抑制外部扰动 dd ,当PC幅值增益越小时，实际输出量 yy可以跟随外部扰动 dd因此综上所述，我们根据闭环这一特点，希望PC幅值增益在低频段增益尽可能足够大，在高频段增益尽可能足够小，进而可以使迫使实际输出量 。

yy 可以跟随给定值 rr，同时可以抑制高频噪声 、低频段的外部扰动n、低频段的外部扰动dn、低频段的外部扰动d P比例控制其中，PID控制是一种闭环控制（反馈控制），P：比例，I：积分，D:微分先从最简单P控制说起：。

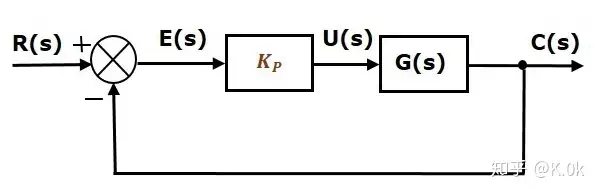
P控制器的数学表达式为： u(t)=KPe(t)u(t)=K_Pe(t) (1)当零时刻，系统偏差 e(t)e(t) 最大，因此 U(t)U(t) 最大,使被控对象输出量快速跟随参考量 r(t)r(t)

，当系统偏差 e(t)e(t) 较小时，由于比例 KPK_P 作用，因此 U(t)U(t) 相应减小，进而减小被控对象输出量然而这种方法是存在稳态误差：根据这个结构可以求得在s域稳态误差和输入信号的关系如下：。

E(s)=R(s)1+KPG(s)E(s)=rac{R(s)}{1+K_PG(s)} (2)其中， G(s)G(s) 为系统的被控对象，这里我们研究LTI的常系数系统，因此 G(s)G(s) 传递函数可以表示：

G(s)=K(s−z1)⋅(s−z2)...(s−zm)(s−p1)⋅(s−p2)...(s−pn)(n≥m)G(s)=Krac{(s-z_1)cdot(s-z_2)...(s-z_m)}{(s-p_1)cdot(s-p_2)...(s-p_n)} (n geq m )

(3)因此，从这个式子也可以提现出，大多数系统的极点都多于零点，具有一定的惯性环节研究给定值为阶跃信号时（ r(s)=1sr(s)=rac{1}{s} ）,代入Eq. (3)于Eq. (2)，且应用终值定理Eq.(4)。

limt→∞E(t)=lims→0sE(s)=11+KPK1lim_{t ightarrow infty}{E(t)}=lim_{s ightarrow 0}{sE(s)}\ =rac{1}{1+K_PK_1}

（4）其中， K1K_1 为被控对象系统的参数，因此可以看出这种P控制器不能让稳态误差为零，然而随着增大 KPK_P 参数，可以减小稳态误差I积分控制因此为了以减小稳态误差为目的，学者们提出了I积分控制。

积分控制是叠加每个时刻的误差信号，因此它具有记忆功能，可以反映一定的历史信息

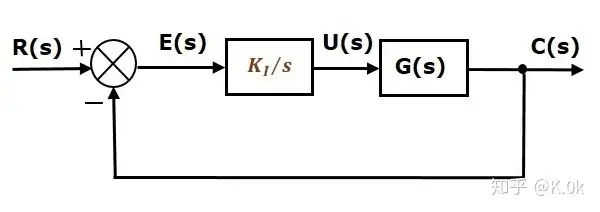
I控制器的数学表达式为： u(t)=KI∫e(t)dtu(t)=K_Iint e(t)dt (5)同理，系统在零时刻，系统偏差 e(t)e(t) 最大，积分进行叠加偏差，直到误差为零，积分输出一个合适的

u(t)u(t) 使被控对象的输出量可以满足需求，因此这种控制可以避免稳态误差根据Eq. (2)和Eq. (4)，应用终值定理可以看出系统的稳态误差为零：limt→∞E(t)=lims→0sE(s)=1

1+KPK1lim_{t ightarrow infty}{E(t)}=lim_{s ightarrow 0}{sE(s)}\ =rac{1}{1+K_PK_1} （6）D微分控制

然而有些场合下，控制会出现一定超调量，如果不想让系统出现超调，可以添加D微分控制环节，微分控制可以反映未来的行为，假设当前系统输出快要到达目标给定，这个时候的误差斜率很大，如果不添加D控制，则会导致超调，但是加入了D控制环节，系统通过对误差微分的作用，可以求得当前时刻误差的降低速度，进而控制误差减小的增速来抑制超调发生。

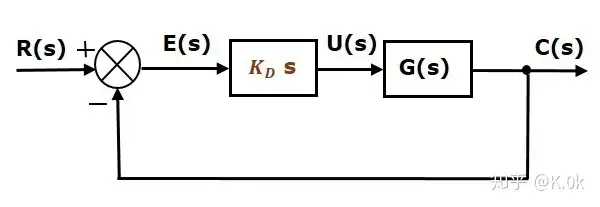
D控制器的数学表达式为： u(t)=KDde(t)dtu(t)=K_Drac{de(t)}{dt} (7)同理，应用终值定理可以看出系统的稳态误差始终为1，因此不能够单独使用PID控制当三个环节都存在的时候，这种控制称为PID控制。

然而系统存在三个参数分别是 、、Kp、KI、KDK_p、K_I、K_D PID控制器的数学表达式为： u(t)=KPe(t)+KI∫e(t)dt+KDde(t)dtu(t)=K_Pe(t)+K_Iint e(t)dt+K_Drac{de(t)}{dt}。

(8)

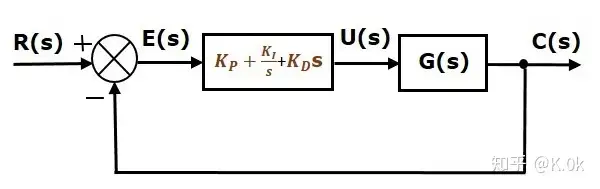
PI控制器具体在实际数字系统中的应用可以参考我这篇文章：PI电流环在数字化实际系统中的完整解析46 赞同 · 18 评论文章实际PID控制器中存在问题问题（一）：积分饱和这里，如果用到积分环节，我们一定或者肯定会存在积分控制器中存在的饱和问题（Anti-windup）：

当系统的达到饱和时，由于积分的作用，系统在对其进行不断叠加，影响退饱和的速度，因此我这里介绍下属两种抗积分饱和的方法：1）：Matlab_tech talk中讲述的一种抗积分饱和方法：

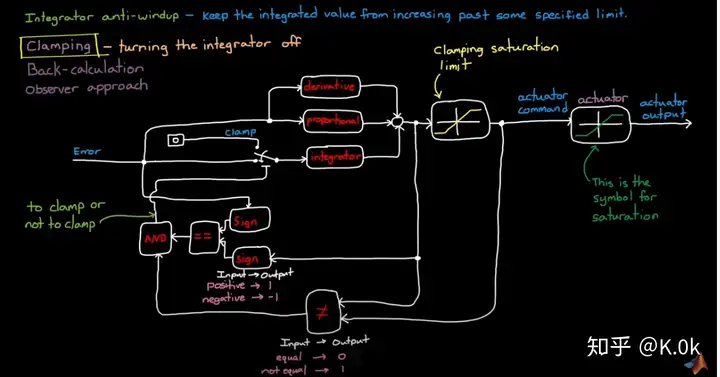
这种方法根据饱和限幅中的输入输出来判断是否一致，如果输入和输出的大小不一致，可以判断系统为输出饱和或当误差值与控制器输出值同号时，系统利用构建的开关来切换到不含有积分通道的系统中（即关闭系统中的积分控制环节）。

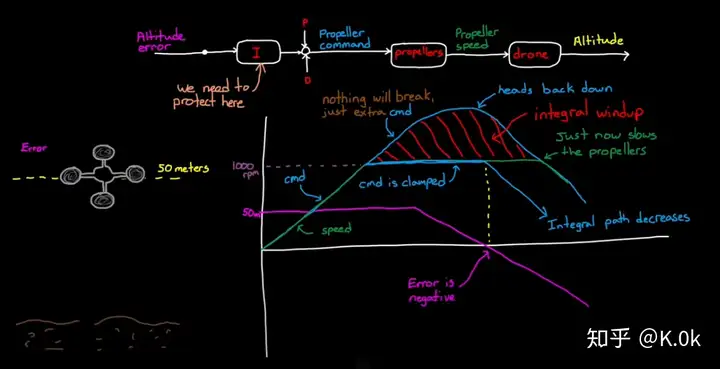
这种方法参考如下所示：https://www.youtube.com/watch?v=NVLXCwc8HzM&list=RDCMUCgdHSFcXvkN6O3NXvif0-pA&index=2​www.youtube.com/watch?v=NVLXCwc8HzM&list=RDCMUCgdHSFcXvkN6O3NXvif0-pA&index=2

2）：TI中用到的抗积分饱和法，详细代码和Pdf手册可参考TI的controlsuiteLib2.0，需要代码或文档资料的也可以评论区留言。

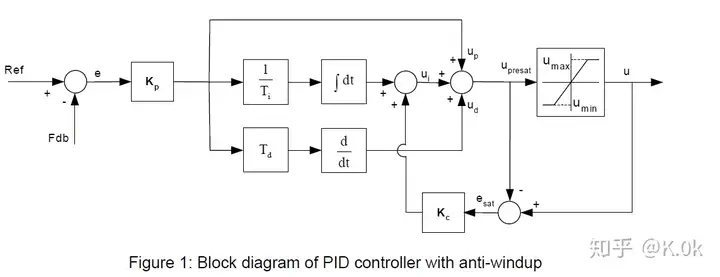
为了便于理解，下式保持TI图中的参数符号，这种方法的带有抗积分饱和的积分控制器可表示为如下所示：

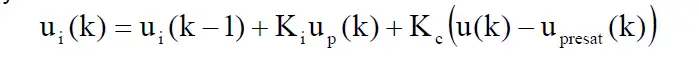
该式在本文中被标记为Eq. (9)其中， KcK_c 代表抗积分饱和系数; 、u(k)、upresat(k)u(k)、u_{presat}(k) 表示饱和限幅函数的输出和输入值; KiK_i 表示积分参数（等同于文中参数

KIK_I ） up(k)u_p(k)可以理解为误差大小问题（二）：高频噪声在实际系统中，微分环节会放大噪声，这个是一个不争的事实，我对其证明如下：对任何一个信号进行傅里叶级数分解：f(t)=a02+∑

n=1∞Cncos(nwt+ϕn)an=2T∫−T2T2f(t)cos(nwt)dtf(t)=rac{a_0}{2}+sum_{n=1}^{infty}{C_ncos(nwt+phi_n)}\ a_n=rac{2}{T}int_{-rac{T}{2}}^{rac{T}{2}}f(t)cos(nwt)d_t

(10)其中， CnC_n 为一个随 nn 变换的参数因此通过上述这个式子可以看出 f(t)f(t) 信号包括直流分量和交流分量，如果这个信号进入到微分环节中，Eq. (10)变为：df(t)dt=−

∑n=1∞Cncnwsin(nwt+ϕn)rac{df(t)}{dt}=-sum_{n=1}^{infty}{C_ncnwsin(nwt+phi_n)} (11)因此我们得出一个结论：当信号频率越高时，经过微分环节后的幅值越大。

在实际的系统中，反馈环节由Sensor构成，其中一定存在一定幅值的白噪声（White noise,一个含有不同频率不同幅值的信号），当白噪声叠加在反馈信号后，通入微分环节，根据上述结论，我们可以发现微分环节会放大高频白噪声的幅值。

事实上，也不一定是白噪声，只要是高频信号，都会被放大那么解决这个问题，一种简单的方法是加入具有低通特性的滤波器最常见的是加入一阶低通滤波器，传递函数如下：Gf(s)=Ns+NG_f(s)=rac{N}{s+N}。

(12)其中 NN 代表截止频率，其倒数就是时间常数，截止频率根据需求设定，从而有效抑制高频噪声另一种方法是在反馈通道中加入积分环节，其方法本质和上述方法一样，感兴趣的朋友可以根据Laplace进行推导，比较简单。

问题（三）：PID参数调节困难常见的PID参数调节有三种方法，第一种是根据经验手动调节法，但这种方法对于新手不太友好且浪费一定的时间比如：增加比例系数可以减小系统上升时间，增加微分系数可以改善系统稳定性并减小超调量等。

第二种为输入一个给定信号（常见的为阶跃信号），观测被控对象的响应特性（响应时间，震荡时间等），然后可以根据Ziegler-Nichols 或者 Cohen-Coon 方法来获得参数但这种方法的缺陷是你需要让你的系统在不稳定的边缘响应，某些设备是不允许这种情况发生的，也会一定概率损坏设备。

第三种为基于模型调参法，这里主要对这种方法进行介绍这种基于模型调参法可以分为以下几种方法零极点配置方法（Pole placement）：利用数学模型获得系统的零极点，把主导极点放到合适的位置回路修正法（Loop shaping）：通过Bode图来评价控制系统，进而获取理想的参数。

启发式法：基于数学模型在软件中来对系统输入一个给定信号，观测被控对象的响应特性（响应时间，震荡时间等），进而获取参数在线调节法：通过在线参数辨识的方法（RLS、LMS、EKF、观测器法等）获取PID相关参数。

这里主要介绍一下前两种方法，两种方法都可以利用MATLAB 中的PID control Design with control system toolbox获取参数(通过软件实现，比较简单)，或者可以利用这两种方法的原理来调节PID参数。

零极点配置法（Pole placement）首先表示PID控制环节中的传递函数，如下所示：u(s)=KDs2+KPs+KIse(s)u(s)=rac{K_Ds^2+K_Ps+K_I}{s}e(s) (13)

可以看出PID控制环节有两个零点（zero），一个极点(pole)且在零点位置，那么对于这种直流电机数学模型（一阶惯性环节），我们只需要利用PI就可以消除被控对象的零点，进而获取PI参数回路修正法（Loop shaping）。

这种方法中，我仅介绍Bode图法，Bode图法也是回路修正法的一种，且在PID整定中被广泛应用（去年在PEMC组的时候，发现意大利博后们就在用这套思路）关于电机控制的调参PID可以看一下这篇文章，这里模型考虑了转速信号和电流信号的滤波，在实际应用中效果也还是不错的：。

A. Lidozzi, L. Solero, F. Crescimbini and A. Di Napoli, "Direct tuning strategy for speed controlled PMSM drives,"

2010 IEEE International Symposium on Industrial Electronics, Bari, 2010, pp. 1265-1270, doi: 10.1109/ISIE.2010.5637034.

由于自己在这上面比较了解，这里就介绍一下这种基于PMSM调PID的bode图方法（基于上述论文的）针对电流环PI控制器，重新定义一下论文中的符号和字母，利用Bode图法基本步骤如下所示：首先计算开环系统传递传递函数：。

这里考虑了逆变器模型及滤波器模型，因此开环传递函数结构图如下所示:

其次PI控制器模型传递函数如下所示：

PI控制器传递函数Eq. (14)其中， K_{p_{-}c} 代表比例系数； K_{i_{-}c} 代表积分系数。逆变器模型传递函数：

逆变器传递函数Eq. (15)其中， T_{dt} 代表死区时间中的延迟环节； T_d 代表开关周期； K_d 代表逆变器的增益。滤波器模型传递函数：

滤波器传递函数Eq. (16)其中， omega_f 代表滤波器截止频率由于上述论文中符号有点混乱，这里我重新定义如下的SPMSM模型传递函数：G_{c_{-}pmsm}(s)=rac{1}{Ls+R}。

（17）其中， L 代表SPMSM定子一相电感; R 代表SPMSM定子一相电阻这里值得注意的是把SPMSM的EMF和耦合项作为扰动项进行处理2. 其次需要满足相角裕度（Phase margin）(当然也要满足幅值裕度（Gain margin）)：。

Eq. (18)其中， arphi_ m 表示相角裕度，这里一定要计算系统开环的传递函数在PI负反馈下，环路增益超过1的时候，arphi_ m 为正数可以保持系统稳定，相位裕度越大，系统越稳定根据相角裕度的定义：在开环系统为0dB增益时，满足Eq. (18)即可。

因此可以列出开环系统为0dB增益的方程：

Eq. (19)因此通过Eq. (18)和Eq. (19)就可以相应的获得PI参数 K_{p_{-}c} 、 K_{i_{-}c} 具体的推导过程也比较简单，这里就不重复介绍了，我做了几组SPMSM的仿真来验证上述利用Bode图方法获取PI参数的有效性。

首先，我为了增加系统的稳定性，我增加相角裕度到60度，如下图：

Bode图

系统闭环电流阶跃给定后的响应曲线从上图，可以看出仿真结果和给定基本接近，保证了系统的稳定性，根据计算，PI参数分别约等于为0.00167，0.0533同样的其它条件下，当减小相角裕度到30度，如下图：

Bode图

系统闭环电流阶跃给定后的响应曲线可以发现相角裕度近似为30度，验证了方法可行性，然而系统稳定性从响应曲线中可以看出下降，如果基于减小相角裕度，系统状态偏差将不能收敛，进而发散，变的不稳定从另一个角度理解，当相角裕度减小，高频的正增益信号相应的增多，进而影响稳定性。

其次，我们还要利用Bode图看另一个判断系统性能的参数：带宽带宽的定义可以参考我这篇文章：上述这篇文章明确指出：BODE图中的穿越频率（穿越频率定义为0dB增益所在处的频率），其大小可以近似等于系统的带宽。

因此我们在计算相角裕度的同时，也就含有穿越频率这个参数，那么在仿真中，令系统的带宽为40Hz(当然实际PMSM驱动系统需求要远远大于这个值，这里只是举个例子)：

Bode图这里对应的是角频率，当转换成带宽，理论和仿真结果一致。

系统闭环电流阶跃给定后的响应曲线根据系统上升时间和带宽的关系，我们也可以看出带宽和之前设定近似一致，根据计算，PI参数分别约等于为0.0119，5.5758。令系统的带宽为400Hz：

Bode图

系统闭环电流阶跃给定后的响应曲线根据上述结果，可以看出带宽增加了10倍根据计算，PI参数分别约等于为0.1397，526.608，可以看出提升带宽，积分系数要增大问题（四）：PID离散化问题由于在实际数字化系统中，采样是不连续的，当采样频率与被控对象变量的基波频率比不够大时，如果利用传统的欧拉公式对其进行离散化会存在较大的误差，进而影响系统控制性能。

因此需要考虑对PID进行z域离散化，进而提高实际数字化PID控制性能常见的z域离散化有如下三种方法，s域直接变换z域法，s域基于Tustin变换z域法,离散化到Z域法具体公式推导可参考我这篇文章，传送门如下：

总结在经典PID控制中，由于自身带有抑制高频噪声及低频外部扰动的能力，因此已经具有了一定的鲁棒性，在实际产品中固然被广泛应用结合现代控制理论和智能控制理论，如今PID已经被发展为模糊PID、增强鲁棒性PID、基于其它算法的PID等。

然而PID的灵魂还是在P、I、D这三个字眼